√70以上 四次元立方体 328376-四次元立方体 インター ステラー
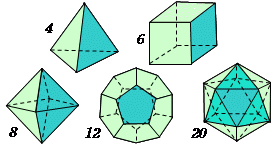
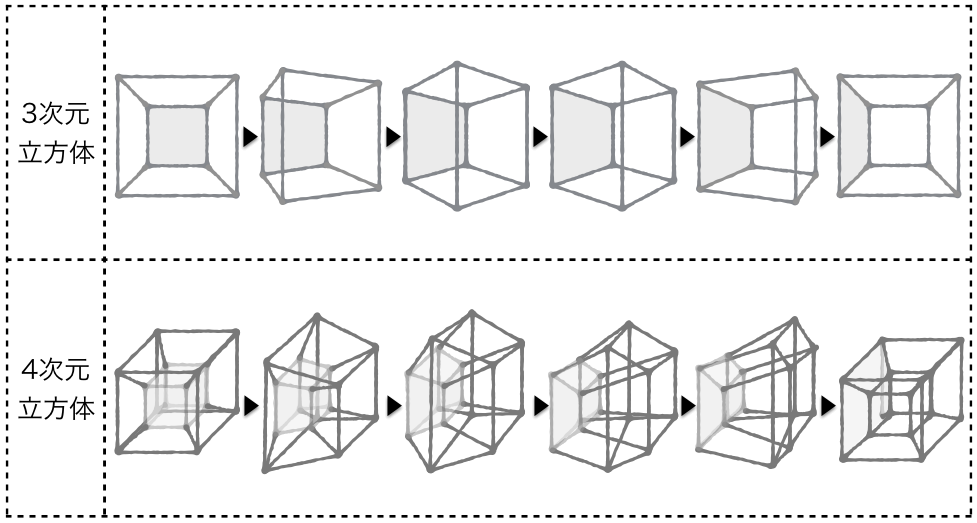
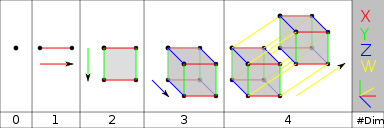
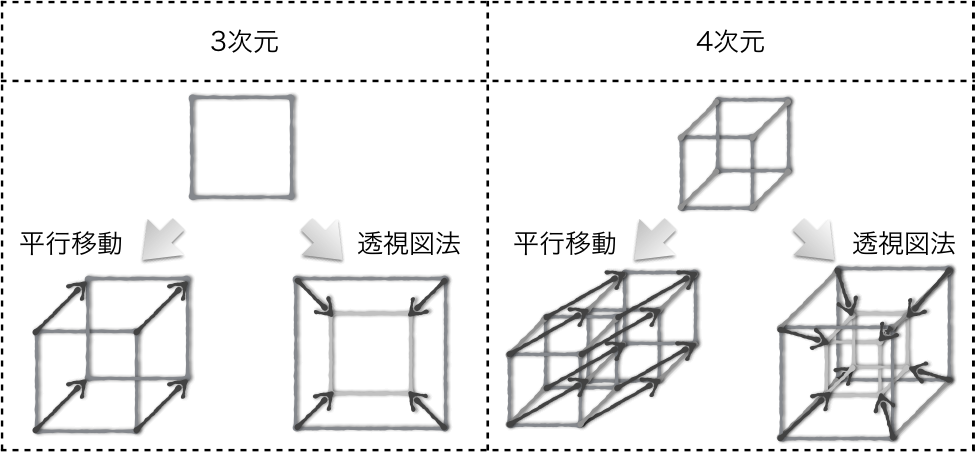
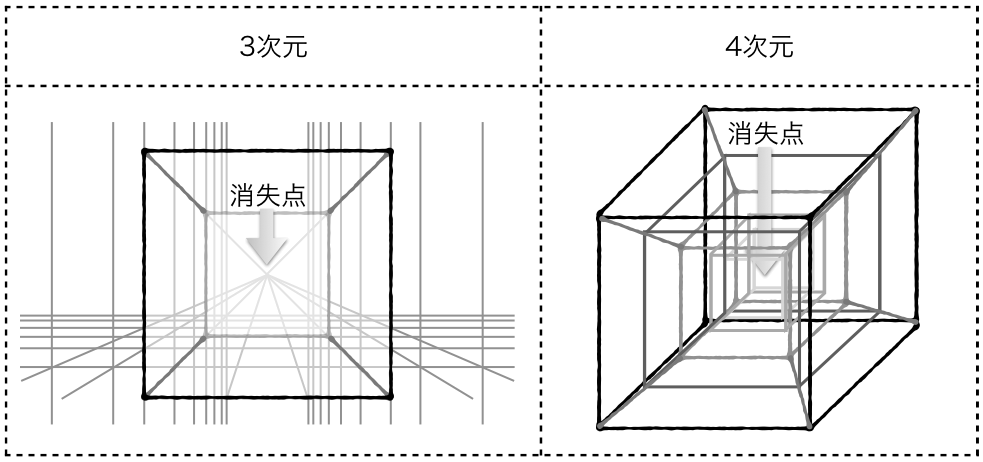
超立方体 (4 次元の 「立方体」) をほぼ30o つつ回転し、 3 次元に 投影した図 (本多、 1994 による) 。 外枠の2 つの立方体の問にある台座みたいな6 個の六面体である。 投影によって 立方体はこのように歪んでしまった。 なぜこのような歪みがおこるかは、 図 4次元の立方体の理解 「4次元の・・」という言葉を見ただけで、ああ、もう理解できるわけがない、と拒絶反応を起こすのが普通かもしれない。 でも、そんなに難しく考える必要はない。 0次元の点、1次元の線、2次元の平面、3次元の立体、と1つずつ次元を上げて行って、もう一つ次元を追加すると4次元になる。 もう1つの次元に、「時間軸」を与える話もある四次元空間についてイメージしてみよう。 流石に球では単純すぎるので,四次元立方体を考える。 三次元立方体からの類推で,各頂点に4本の,お互い直交した同じ長さの辺が交わる立体が四次元立方体だと定義する。 2,3,4次元立方体の構成要素を比較しよう。
超立方体5次元
四次元立方体 インター ステラー
四次元立方体 インター ステラー-Mixi算数話 4次元の立方体 はじめまして tuttiといいます。小学校算数の少人数やってます。 こもっちゃんさんのご紹介でトピ立てさせていただきます。 以下私の日記から・・ 「先日、算数の勉強会があって行ってきました。 会の宿題が 1 立方体が47個の立方体に分割できない理由 2 図のような立方体125個でできた立方体を図の点a,b,cを通る平面で切 3 3次元の物体、例えば正四面体の頂点のデータを取得したとします。正四




8j9bmz8vvktdlm
シュタイナーの四次元その25 カテゴリ: 神秘体験空間 次に、正方形を考える。 それが空間中を移動して立方体が描かれると想像する。 正方形の動きはそれが最初にあった位置に対して垂直である必要がある。 立方体はその面を構成する6つの正方形4次元の立方体って・・・? 3次元の立方体を、スーッと(べつの次元に1だけ)もちあげると、 (4次元なんて、どこにもちあげていいのやら・・・) 4次元の立方体(超立方体)ができるはずです。 これを、4次元の立方体、つまり超立方体ということにしましょう。 (色のつけ方ひとつで、ずいぶんとちがって見えるものですね。 ほかに、いくつ立方体が見えますか?4次元空間の立方体 hypercube 4次元ユークリッド空間で (1, 1, 1, 1) および座標の符号を変えた16個の点を 頂点にもつ. (±1, ±1, ±1) (±1, ±1, ±1, ±1) (±2, 0, 0) (±2, 0, 0, 0) τ = 1 √ 5 2 (±1, ±τ , 0) 頂点の
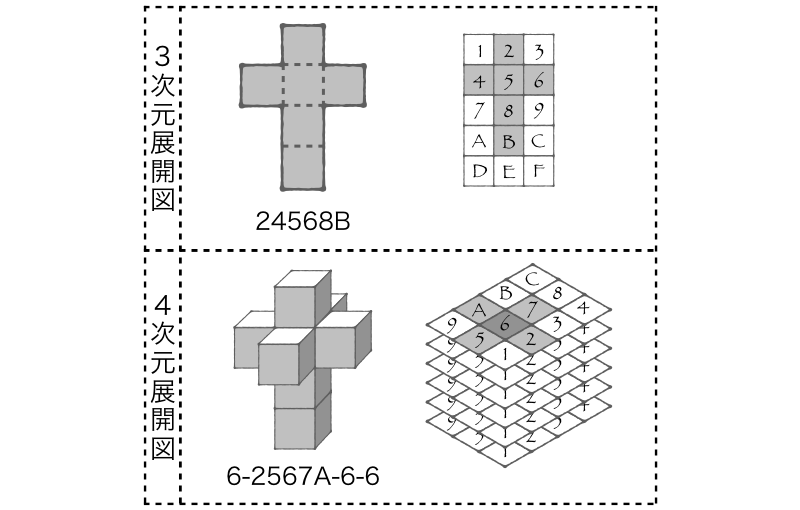
四次元準立方体詩派宣言 詩集 著者 渋江周堂 著 出版者 豚詩社 出版年月日 昭13 請求記号 書誌ID(国立国会図書館オンラインへのリンク) DOI / 公開範囲 国立国会図書館/図書館送信参加館内公開 詳細表示 資料種別 (materialType) Book正八胞体(せいはちほうたい、または四次元超立方体、8cell、octachoron、tesseract)とは、四次元 正多胞体の一種で8個の立方体からなる、四次元の超立方体である。 胞(構成立体):立方体8個 面:24枚の各正方形に立方体2個が集まる。; C'Thiris Tesseract You can not craft(クティリスの四次元立方体がクラフトできない) こんにちわ、私は日本人です日本人でこの解決法を知ってる方がいたら教えてください 4に強化してもクティリスの四次元立方体がでないのですがなぜでしょう探してる間に
四次元への扉へ戻る 次 四次元図学 三次元の立方体はさいころのような形として容易に認識できる。立方体を三次元空間とは垂直の第四の軸方向にぎゅーっと引き伸ばすと四次元超立方体の出来上がり、ということで、私も小学校のころに以下のような図をどこかで見たと思う。3月25日(日) 四次元立方体の展開図を三次元空間に隙間なく並べる 3月日のひとことでご紹介している、立方体を単位とした三次元の網目の構造を、四次元立方体の展開図で作る話です。 こんな風に並Many translated example sentences containing "四次元超立方体" – EnglishJapanese dictionary and search engine for English translations



入門 古埃及女祭司的靈魂旅程 7 網上導讀會 宇宙的奧秘 30 35章 怡然之光 新浪博客



正多面体の体積 高精度計算サイト
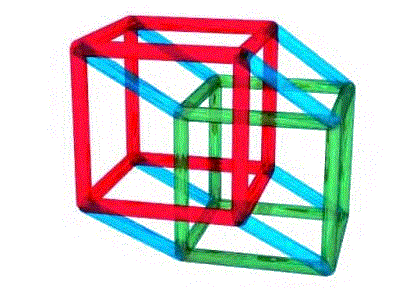
『四次元の立方体万華鏡 cumos 』展 日時 • 07 年 11 月 26 日 (月) 〜 12 月 7 日 (金) 11 日間 テーマ 「 cumos(キューモス) の点線面」 ヤマザキミノリが 1974 年、芸大1年時に考案し、 80 年代に世に送り出した幻の立方体万華鏡が螺旋時空の上に復活しました。巨大 四次元超立方体さいころの展開図 / Development of FourDimensional Hypercube (Tesseract) Dice 解説・講座 四次元超立方体さいころの展開図です。四次元空間のさいころはこの展開図を組み立てた超立方体すな 4次元の超立方体は、 立方体(赤)と立方体(緑)と立方体の6面の軌跡が作る6個の立方体、 合計で8個の立方体に囲まれた図形です。 残念ながら3次元しか認識できない私達にとっては、 8個の立方体が重なって見えるだけです。




一人称からの四次元迷路



4次元の立方体を描く
4次元立方体の展開動画 24年以上前に学術誌 数理科学に高次元立方体の表現という論文を掲載させていただきました。 その時の4次元立方立方体を x y z それぞれに対し、垂直な w の方向に動かすと、その軌跡は超立方体になる。超立方体は八つの立方体と二十四の面と三十二の辺と16個の頂点を持っていることになる。 ところで、次元と言えば世の中の図形パズルの主流は二次元パズルである。 超立方体のブロック積みの頂点と、それぞれの超立方体の中心を結ぶ(つまり体心立方格子)とokなのだが、そもそも超立方体を積み上げる作業が三次元人には容易ではない。 正24胞体 {3, 4, 3} 四次元独特の均整の取れた立体。



cks ブックス 4次元立方体の開き方



四次元超立方体 Bykrs745
完全に見た目が同じですね。 もしこの他にも4次元の要素を見つけた方は教えて頂けると嬉しいです! さぁ今回の小ネタはこの辺で終わりにしましょう。 塩ラーメンのエヴァ研究室では、皆さんのご意見をお待ちしております。 ①AmebaOwndにログインして4次元超立方体は、つぎの8個の立方体でできている 黄色 (1個):移動前の立方体 緑色 (6個):正方形が移動してできた立方体 青色 (1個):移動後の立方体 立方体の展開図 と見比べると、この4次元超立方体の形を思い浮かべられるようになるかもしれません。 つぎは、最後の画面です。 4次元超立方体 立方体万華鏡 cumos キューモスは、いわゆる三角柱型の普通の万華鏡とは違い、無限宇宙イメージが三次元空間に拡がるタイプです。 1974年にヤマザキミノリが開発したオリジナルで1985年に実用新案を取得しました。
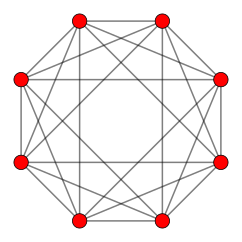



多胞体 Wikiwand




正八胞体 Wikipedia



不同维度的对话 带你进入四维世界 Matrix67 The Aha Moments



cks ブックス 4次元立方体の開き方



차원 次元 Dimension



四次元世界 qazのつれづれ日記



cks ブックス 4次元立方体の開き方



超立方体




立方体 の新着タグ記事一覧 Note つくる つながる とどける



不同维度的对话 带你进入四维世界 Matrix67 The Aha Moments



4次元の立方体を描く




四維超正方體 维基百科 自由的百科全书



無料ダウンロード 4次元超立方体 かわいいフリー素材集いらすとや




デッサンの基礎 光と陰影 美大受験予備校 難関美大への現役合格なら横浜美術学院




一些距离表示和相似度量 台部落



色の知覚2




正八胞体 素数交響曲第2番




立方體 幾何圖形 定義 立方體特徵 幾何性質 聯繫 套用 日常生活 遊戲 視錯覺 中文百科全書



四次元空間球 Waka Lab Charlie W




Pythonモジュール ライブラリ Numpy編3 値の取り出し しろちゃのプログラミング日記



多胞体 Owlapps



Rで球面幾何学 オイラーの多面体定理 Euler S Polyhedron Theorem と平面充填 Tiling の連続性について Qiita



2次元と4次元を科学する



立方体 全国180中学の入試算数 解法研究



cks ブックス 4次元立方体の開き方



没有基础学画动漫插画 是应该从哪方面开始学起 素描吗 知乎



グラフ さんすう 数学のお勉強



立方体 快懂百科



不同维度的对话 带你进入四维世界 Matrix67 The Aha Moments




次元 Wikiwand



不思議な連続写像たち 応用数理学科 小山晃 早稲田大学 基幹理工学部 研究科




多胞体 Wikiwand




デッサンの基礎 光と陰影 美大受験予備校 難関美大への現役合格なら横浜美術学院



干货分享 游戏场景管理的八叉树算法解析 It S Time Csdn博客




Threes タオル 18 2 26 Booth




Images Of 正八胞体 Japaneseclass Jp



高次元とは目に見えない世界ですか 三次元も含むなら一部見えますか Yahoo 知恵袋



シュタイナーの四次元その25 シュタイナーから読み解く神秘学入門 楽天ブログ




魂の自分 肉体の自分 そして宇宙の自分 私的な備忘録的な何か



多维空间真的存在吗 特有理 万维博客




四维空间 维基百科 自由的百科全书



多维空间真的存在吗 特有理 万维博客




立体描画と処理 Wolfram言語ドキュメント




結晶構造 Wiki 日本語 Japanese Study In China




ハイパーキューブとは何ですか その定義と意味 21



设计癖 这个堪称 宜家智库 的实验室 除了教你智能摆摊 还有哪些脑洞创意



时间是第三维吗 科学小本子



無料ダウンロード 4次元超立方体 かわいいフリー素材集いらすとや



フラットランド 四次元の世界 そして相対性理論 なおきのブログ




8j9bmz8vvktdlm



超立方体5次元



2次元と4次元を科学する



靠数学 拿了 两次诺贝尔奖 彭罗斯从 铺地砖 帮忙发现11年化学奖的秘密 量子位 Csdn博客



第一章 宇宙の構造




3次元の立体は2次元の平面で表現出来ます ならば4次元空間は3次元で表現出来ないのでしょうか Quora




正八胞体 Wikipedia



3次元トーラス 四元数多様体 Etc




Knznymmmy Code777 4d を読んだ



大老李聊数学 全集



時間と別れるための50の方法 ページ 4 Cave Syndrome



この世界は3次元 時間の4次元で出来ていると聞きますが 空間と時間は直行しているということですか Quora




四次元立方体の断面動画 完全無欠で荒唐無稽な夢



4次元の立方体を描く



超立方体 6次元



差異と反復 7 Cave Syndrome



その55 そもそも W って何なのか
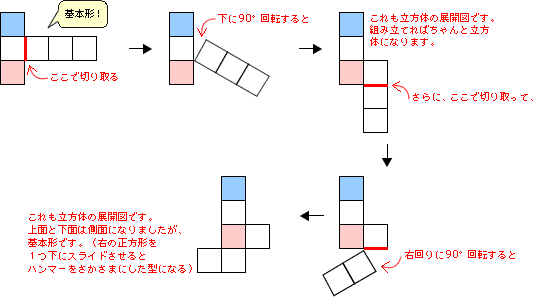



最高の立方体展開図 何種類 最高のぬりえ




四角錐台の体積 高精度計算サイト




立方体とは サイエンスの人気 最新記事を集めました はてな




Moss06es8db3jm



17 5 15 梅塔特隆立方體 寶瓶世紀聖哲曼學院 痞客邦



無料ダウンロード 4次元超立方体 かわいいフリー素材集いらすとや



经典再读 生命之花 灵性法则の第六章下 自由微信 Freewechat



立体描画と処理 Wolfram言語ドキュメント




Tシャツ 四次元超立方体さいころの展開図 波間のかけひき Booth




結晶構造 Wiki 日本語 Japanese Study In China



正射影 空間の必須手法




タカハシタカスケ Tahatasu Twitter




正八面体 正八面体の概要 Weblio辞書



シュタイナーの四次元その18 シュタイナーから読み解く神秘学入門 楽天ブログ
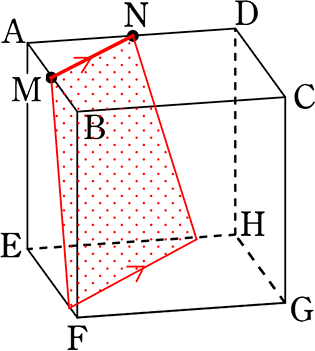



中学数学 空間図形




正十二面体の中に立方体 アットランダム ブリコラージュ 転ぶな 風邪ひくな 義理を欠け 長寿の心得 岸信介 食う 寝る 出す 風呂 在宅生活4つの柱



無料ダウンロード 4次元超立方体 かわいいフリー素材集いらすとや



シュタイナーの四次元その15 シュタイナーから読み解く神秘学入門 楽天ブログ



未调频四次元立方体 Unattuned Tesseract Te3 热力膨胀3 Thermal Expansion 3 Mc百科 最大的minecraft中文mod百科



火卫二锡矿石 Tin Ore Gs 星空 Galaxy Space Mc百科 最大的minecraft中文mod百科




結晶構造 Wiki 日本語 Japanese




熱放射の理論1 ステファン ボルツマンの法則 Note



动画效果 然后顺便介绍了



Scp 2634 Scp基金会



四次元




問題129
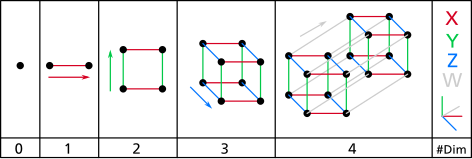



維度 Wikiwand
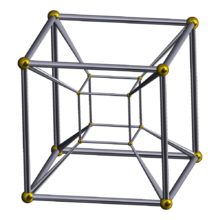



四維超正方體 维基百科 自由的百科全书



コメント
コメントを投稿